代用電荷法(基本解近似解法)
Charge Simulation Method (Method of Fundamental Solutions)

Stokes flow past a planar square array of spheres computed by the fundamental solution method based on the periodic fundamental solution.I am grateful to Mr. Daisuke Matsuoka (Graduate School of Science and Engineering, Ehime University) for his help in making this figure.
科学技術問題を数理的に扱おうとすると、必ずといっていいほど、偏微分方程式があらわれます。 偏微分方程式の解を厳密に得る場合はまれで、ほとんどの場合、数値的に解を求めることになります。 偏微分方程式の数値解法としては、有限要素法、差分法が代表的なもので多くの研究がなされています。 私達の研究室で研究している代用電荷法も偏微分方程式の数値解法のひとつであり、 とくにポテンシャル問題(流体力学、電磁気学などに現れます)によく用いられます。 そして、次のようなよい性質を持っています。
- プログラミングが簡単。
- 計算量が少ない。
- ある条件下では真の解への収束が速い。
ポテンシャル問題に対する代用電荷法
では、これから代用電荷法について具体的に説明します。 を2次元平面または3次元空間内の領域として、 領域
における次のポテンシャル問題、すなわち、 ラプラス方程式の境界値問題を考えます。
ここで、は領域
の境界、
は境界
上で与えられた関数です。 代用電荷法では、この境界値問題の解を次の形で近似します。
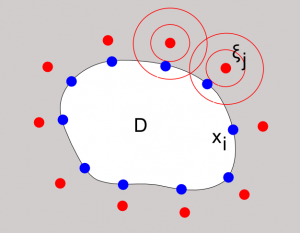
図1:代用電荷法のイメージ
ここで、近似解 は領域
でラプラス方程式
を満たすことに注意しましょう。 つまり、代用電荷法においては、近似解は問題となっている偏微分方程式(ここではラプラス方程式)を 厳密に満たすのです。 一方、境界条件については、条件を少し緩めて、次の拘束条件を満たすようにします。
ここで、は 境界
上にユーザによって与えられた点であり、 拘束点と呼びます(表1参照)。 拘束条件は電荷
に対する連立1次方程式
を成し、 この連立1次方程式を解くことにより電荷 が定まります。
代用電荷法の一般化
これまで説明したポテンシャル問題に対する代用電荷法は, 他の問題(波動問題,流体力学,弾性問題など)に応用することができます。
ポテンシャル問題に対する代用電荷法では,近似解は
と表され, が
で
を満たす, もっと正確に言えば,
を満たすことから, 近似解 がラプラス方程式
を厳密に満たします。
この点に着目して,代用電荷法の一般化を考えてみます。 を線形偏微分作用素,
を2次元平面または3次元空間内の領域として, 次の斉次偏微分方程式の境界値問題を考えます。
この偏微分方程式に対し, を方程式
の解とします。 を偏微分作用素
の基本解と呼びます。 そして、いま考えている偏微分方程式の境界値問題に対し、次の形の近似解を考えます。
ここで, は領域
は外部にユーザによって与えられた点であり, ソース点と呼びます。
はすぐあとで述べる方法により定める定数係数です。
近似解 は領域
で偏微分方程式
を厳密に満たすことに注意しましょう。
境界条件については、もとの条件を緩めた拘束条件
を近似解に課すことにします。 ここで、 は境界
上にユーザによって与えられた点であり,拘束点と呼びます。 拘束条件は
に関する連立1次方程式
をなし、この連立1次方程式を解くことにより係数
が定まります。
以上で述べたのが代用電荷法の一般化です。 このように、ポテンシャル問題以外の問題に一般化した代用電荷法は基本解近似解法 (method of fundamental solutions)と呼ばれることが多いです。
例として、2次元波動問題に対する代用電荷法(基本解近似解法)の応用について述べます。
速度 で伝搬する2次元波は、2次元波動方程式
で記述されます。 (
は角振動数)と変数分離すると、 ヘルムホルツ方程式
を得ます。波動問題はこのヘルムホルツ方程式を解く問題に帰着されることが多いです。 そこで、 を2次元平面内の外部領域として、 次のヘルムホルツ方程式の境界値問題を考えます。
ここで、 は境界
上で定義された関数、 3番目の式はゾンマーフェルトの外部放射条件であり、外部波動問題を考える時標準的に課される条件です。
いまの場合、ヘルムホルツ作用素 の基本解は、
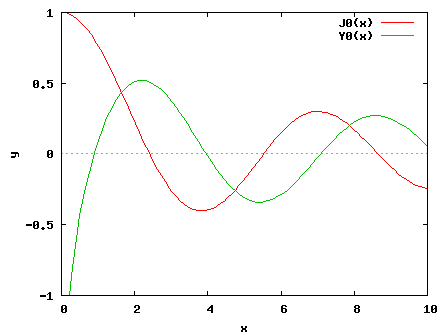
図2:ベッセル関数
したがって、上の境界値問題に対して代用電荷法(基本解近似解法)の近似解は次の形となります。
ここで、は 領域
外部にユーザによって与えられたソース点、
は定数係数であり、上に述べたように拘束条件を 課すことにより定めます。
物理的なイメージでいうと、近似解は点
に波源をもつ2次元球面波を重ねあわせたものとなります(図3参照)。
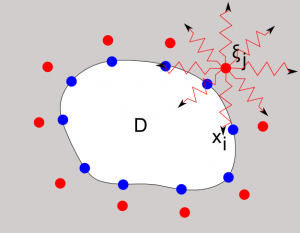
図3:波動問題に対する代用電荷法のイメージ
図4は、円柱によって平面波が散乱される様子を、基本解近似解法によって計算したものです (図では円柱は描かれていませんが)。
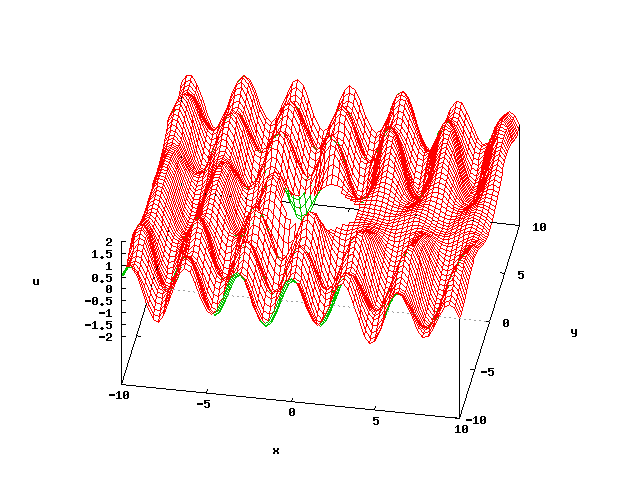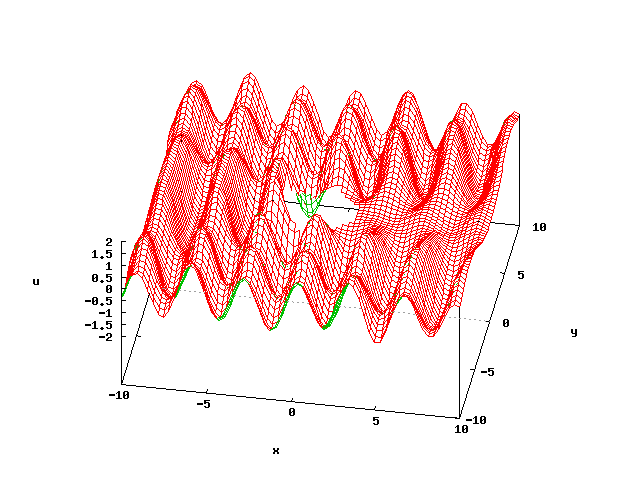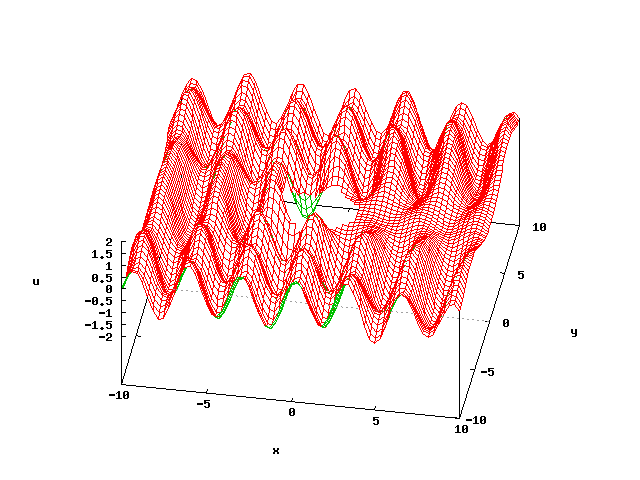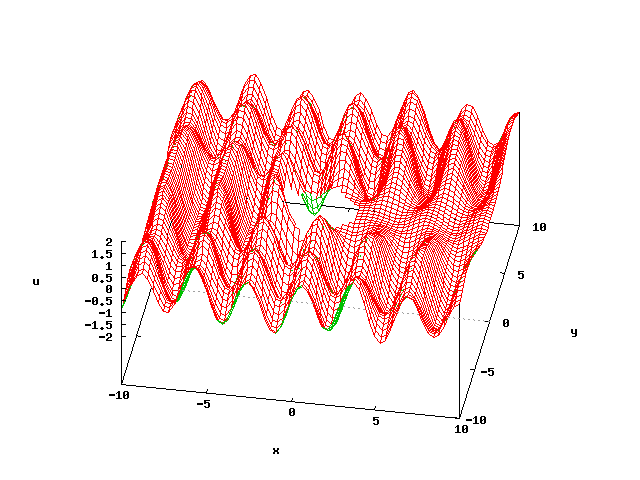
図4:円柱による平面波の散乱
代用電荷法に関する我々の成果と現在の研究
緒方研究室における代用電荷法に関する研究業績には下記のものがあります。
- 空間周期的問題に対する代用電荷法の拡張。
上の図は、球体の3次元無限格子を過ぎる粘性流(ストークス流)の様子を表します。 - 圧縮性流問題に対する代用電荷法。
- 代用電荷法による流体解析(ポテンシャル流の圧力解析など)。
- 波動問題(ヘルムホルツ方程式)に対する代用電荷法,理論誤差評価と数値実験。
- 高速多重極展開およびGPUコンピューティングによる代用電荷法の高速計算。
- 代用電荷法による逆問題解析。
