佐藤超函数論に基づく数値解析

佐藤超函数論に基づく数値解析
Numerical Analysis Based on the Hyperfunction Theory

$\delta(x) = - \frac{1}{2\pi\mathrm{i}} \left( \frac{1}{x+\mathrm{i}0} - \frac{1}{x-\mathrm{i}0} \right).$

デルタ関数の佐藤超函数論における表示

現代物理学にはデルタ関数といった従来の関数の枠から外れた関数が用いられ，これを数学的に正当化するために「超函数」というものが考案されています．超函数には，シュワルツ超函数，佐藤超函数の二つの流儀がありますが，ここで取り上げるのは後者の佐藤超函数です．

佐藤超函数とはどういうものか，一言で言いますと，極，不連続，デルタ関数といった特異性を持つ関数を複素解析関数で表したものです．数値計算において，特異性をもつ関数は一般的に精度が悪くて扱いにくい．一方で，解析関数は制度が良くて扱いやすい．扱いにくい特異性のある関数を扱いやすい解析関数で表すという佐藤超函数の側面は応用上重要・有用であると考え，私たちは佐藤超函数に基づいた数値解析の研究を行っています．

ここでは，数値積分を例に佐藤超函数の数値解析の応用について解説します．

佐藤超関数論

まず，佐藤超函数の定義を端的に述べます．

佐藤超函数(hyperfunction)とは複素正則関数の境界値の差です．

つまり，実軸上の区間 I における超函数 f(x) とは， I 近傍のある複素領域において I を除いて正則である複素関数 F(z) を用いて，

$$f(x) = F(x+\mathrm{i}0) – F(x-\mathrm{i}0)$$

と表される一般化関数です．
そして，複素正則関数 F(z) を超函数 f(x) の定義関数と呼び，f(x) = [F(z)] と記します．

代表的な佐藤超函数の例を次に挙げます．

ディラックのデルタ関数．
$\delta(x) = - \frac{1}{2\pi\mathrm{i}} \left( \frac{1}{x+\mathrm{i}0} - \frac{1}{x-\mathrm{i}0} \right).$ 　(*)
ヘヴィサイドのステップ関数． $H(x) = \begin{cases} 1 & :\: x > 0 \\ 0 & :\: x < 0 \end{cases} = \left[ - \frac{1}{2\pi\mathrm{i}}\log(-z) \right],$
ただし，log z は z が正の実数のとき実数値を取る主値であるとします．
非整数べき乗． ${x_+}^{\alpha} = \begin{cases} x^{\alpha} & :\: x > 0 \\ 0 & :\: x < 0 \end{cases} = \left[ - \frac{(-z)^{\alpha}}{2\mathrm{i}\sin(\pi\alpha)} \right] \quad ( \: \alpha\neq 0,\pm 1,\pm 2,\ldots \: ),$
ただし， $z^{\alpha}$ は z が正の実数のとき正の実数値を取る主値であるとします．

図1にヘヴィサイドのステップ関数 H(x) の定義関数 $F(z) = - \frac{1}{2\pi\mathrm{i}}\log(-z)$ の実部の3次元グラフを示します．実軸上の境界値の差がステップ関数 $H(x)$ を与えていることがよくわかると思います．

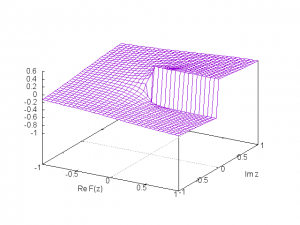
20160923002deffunc

図1：ヘヴィサイドのステップ関数の定義関数の実部．

ディラックのデルタ関数が式(*)のように表されるのは，次のように考えれば理解できます．
まず，f(z) を複素平面の原点O近傍で正則な複素関数としますと，コーシーの積分公式より次が成り立ちます．

$\frac{1}{2\pi\mathrm{i}}\oint_C \frac{f(z)}{z}\mathrm{d}z = f(0),$
ここで，C は原点 O の周りを正の向きに囲む閉積分路で，C およびその内部で f(z) は正則であるとします（図2参照）．

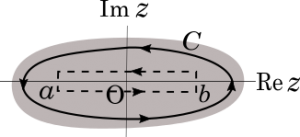
integral_path_origin

図2：複素平面内の原点 O を正の向きに囲む閉積分路 C．

コーシーの積分定理より，複素積分路 C は被積分関数が正則である範囲で自由に変形できるので，図2のように実軸の区間 (a,b) (a < 0 < b) を上下から挟むような積分路に変形します．すると，

$- \frac{1}{2\pi\mathrm{i}}\int_a^b \left(\frac{1}{x + \mathrm{i}0} - \frac{1}{x - \mathrm{i}0} \right)f(x)\mathrm{d}x= f(0)$
を得，デルタ関数の定義より

$\int_a^b \delta(x)f(x) \mathrm{d}x = f(0) = - \frac{1}{2\pi\mathrm{i}}\int_a^b \left( \frac{1}{x+\mathrm{i}0} - \frac{1}{x-\mathrm{i}0} \right)f(x)\mathrm{d}x$
となります．これが任意の関数 f(x) に対して成り立つので，式(*)を得ます．

区間 I 上の超函数 f(x) = [F(z)] に対し，その I 上の積分は次で定義します．

$\int_I f(x)\mathrm{d}x = - \oint_C F(z)\mathrm{d}z,$
ただし，C は区間 I を正の向きに囲む閉積分路とし，定義関数 F(z) は C およびその内部で正則であるとします．デルタ関数の時と同様に，閉積分路 C を区間 I を上下から挟む細長い長方形に変形すれば，

$\int_I f(x)\mathrm{d}x = \int_I \{ F(x+\mathrm{i}0) - F(x-\mathrm{i}0) \}\mathrm{d}x$
を得，超函数の定義と符合することがわかります．

佐藤超函数論の数値積分への応用

さて，いよいよ，数値解析への応用の話に移ります．

まず，次の形の積分を考えます．

$\int_I f(x)w(x)\mathrm{d}x,$
ここで，I は実軸上の区間，f(x) は I 上の実解析関数（I を含むある複素領域で正則な関数）， w(x) は重み関数です．このとき，被積分関数は次のように超函数とみなすことができます．

$\chi_I(x)f(x)w(x) = \left[-\frac{1}{2\pi\mathrm{i}}f(z)\Psi(z)\right] = - \frac{1}{2\pi\mathrm{i}}\left[f(x+\mathrm{i}0)\Psi(x+\mathrm{i}0) - f(x-\mathrm{i}0)\Psi(x-\mathrm{i}0)\right],$
where $\chi_I(x) = \begin{cases}1 & :\: x\in I \\ 0 & :\: x\not\in \overline{I},\end{cases}\quad\Psi(z) = \int_I \frac{w(x)}{z-x} \mathrm{d}x.$
したがって，超函数積分の定義より考えている積分は次のように複素積分表示されます．

$\int_I f(x)w(x)\mathrm{d}x = \frac{1}{2\pi\mathrm{i}}\oint_C f(z)\Psi(z)\mathrm{d}z.$ 　(#)

ここで，C は区間 I を正の向きに囲む閉積分路です．式(#)右辺の複素積分を台形則で近似することにより，次の近似積分公式を得ます．

$\int_I f(x)w(x)\mathrm{d}x = \frac{1}{2\pi\mathrm{i}}\int_0^{u_{\rm p}}f(\varphi(u))\Psi(\varphi(u))\varphi^{\prime}(u)\mathrm{d}u \simeq \frac{h}{2\pi\mathrm{i}}\sum_{k=0}^{N-1}f(\varphi(kh))\Psi(\varphi(kh))\varphi^{\prime}(kh)$ $\left( \: h = \frac{u_{\rm p}}{N} \: \right).$

(★)

ここで，閉積分路 C を周期 u_p の周期関数 $\varphi(u)$ を用いて， $C : \: z = \varphi(u)$ とパラメータ表示しました．式（★）による数値積分公式を超函数法と呼びます[3]．

なお，式（★）の形の数値積分公式は，我々より前に平山氏が提案しています[1]．しかし，文献[1]では佐藤超函数との関連については言及されていません．

ところで，式（★）の数値積分は，積分区間の周りを行って戻る閉積分路上に標本点をとるので，通常の数値積分公式よりおおよそ倍の標本点数が必要になります．
しかし，被積分関数 f(x) が実軸上実数値ならば，複素正則関数に対する鏡像の原理を用いて，標本点数を半減させることができます．

数値例

次の積分を，超函数法（鏡像の原理により標本点数を半減した公式）およびDE公式[4]で計算しました．

$\int_0^1 \mathrm{e}^x x^{\alpha-1}(1 - x)^{\beta-1}\mathrm{d}x = F(\alpha; \alpha+\beta; 1) \quad ( \: \alpha, \beta > 0 \: ),$
ここで，F(a;b;x) は合流型超幾何関数です．
DE公式は実際の科学技術計算でよく用いられる数値積分公式で，とくに端点特異性をもつ積分に対して有効とされています．

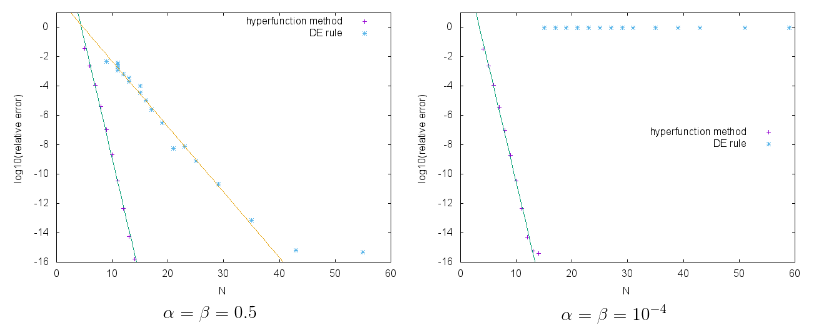
$\alpha = \beta = 0.5, 10^{-4}$ の場合に両公式で積分計算し，その誤差の標本点数 N に対する変化を図3に示します（”hyperfunction method”=超函数法，”DE rule”=DE公式）．

図3：超函数法およびDE公式の誤差．

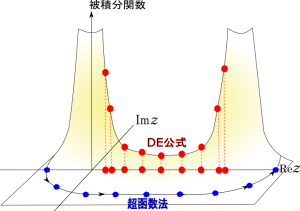
integrand

図4：超函数法およびDE公式の標本点．

図から分かるように，超函数法の方がDE公式より速く誤差が減衰しています．とくに， $\alpha=\beta=10^{-4}$ と端点特異性が非常に強い場合，DE公式では積分計算が全然できていませんが，超函数法ではちゃんと積分計算ができています． DE公式は端点特異性のある積分に強い公式として知られていますが，このように特異性が非常に強い場合は計算できないことがあります．しかし，そのような場合でも超函数法はちゃんと積分計算ができているのです．

その理由は次のように考えられます．
DE公式では，標本点を積分区間端点に集積するようにとっているので（図4参照），端点特異性のある積分に強くなっているのです．しかし，今の場合のように端点特異性があまりにも強いとそれが仇になり，特異性のある端点近傍で巨大な積分値を多くの標本点で計算することになり，それで計算がうまくいかなくなると考えられます．
一方，超函数法の場合，特異点のある端点を避けて，被積分関数の値が穏やかに変化する複素平面上に標本点を取っているので，積分値が精度良く計算できるのです．

はじめに超函数とは，特異性のある関数を解析関数で表したものと言いました．超函数法では，その解析関数（すなわち，超函数の定義関数）を利用して，特異性をもつ関数の情報を集めて数値積分を行っているのです．

＊DE公式で端点特異性の非常に強い積分が計算できない理由について，その詳細は文献[3]に記してあります．

まとめ

ここでは，有限区間積分の数値計算だけを取り上げて，佐藤超函数論の数値解析への応用を示しました．
超函数法は，その他，無限区間積分，アダマール有限部分積分の数値計算にも応用できます．
また，今後は数値積分以外にも今後，フーリエ変換，積分方程式などへも佐藤超函数論の応用を考えていきたいと考えています．

なお，数値解析と佐藤超函数論の関連については，森による先行研究[2]があります．文献[2]では，超函数法で用いた実積分の複素積分への変換式(#)について，核関数 $\Psi(z)$ を連分数展開し，それを有限項で打ち切ることにより，ガウス・ルジャンドル数値積分公式など既存の数値積分公式が導出できることなどが指摘されています．

参考文献

[1] 平山弘，周回積分変換法による数値積分法，第44回数値解析シンポジウム講演予稿集，(2015)，21–24．

[2] 森正武，数値解析と超函数論，京都大学数理解析研究所講究録，145 (1972) 1–11．

[3] 緒方秀教，平山弘，数値積分に対する超函数法，日本応用数理学会論文誌，Vol.26 (2016) 33–43．

[4] H. Takahasi and M. Mori, Double exponential formulas for numerical integration, Publ. RIMS Sci. 9 (1974) 721–741.